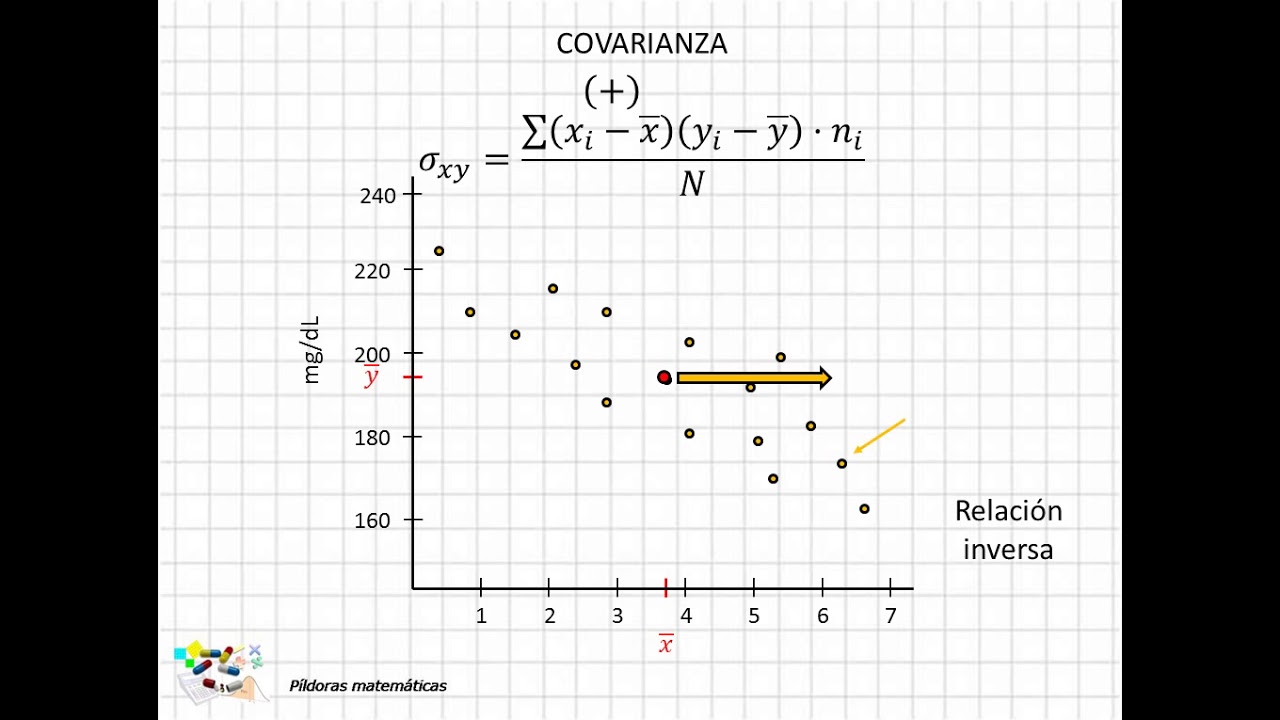
La Covarianza Puede Ser Negativa

La covarianza es un concepto importante en estadísticas y análisis de datos que describe la relación entre dos variables. Si el valor de la covarianza entre dos variables es negativo, sugiere que cuando una variable aumenta, la otra tiende a disminuir. Veamos más a fondo cómo se manifiesta esta situación.

Entendiendo la Covarianza

Antes de sumergirnos en la idea de una covarianza negativa, es crucial comprender qué es exactamente la covarianza. En pocas palabras, la covarianza es un valor que indica cómo dos variables diferentes se mueven en relación una con la otra. Si la covarianza es positiva, significa que las variables tienden a moverse en la misma dirección, mientras que una covarianza negativa indica que las variables se mueven en direcciones opuestas.

¿Por qué la Covarianza Puede Ser Negativa?

Una covarianza negativa puede surgir por diversas razones, pero una explicación común es la presencia de una relación inversa entre las dos variables analizadas. Por ejemplo, en un escenario donde se compara la temperatura ambiente con la cantidad de nieve en un determinado lugar, es probable que exista una covarianza negativa, ya que a medida que la temperatura aumenta, la cantidad de nieve tiende a disminuir. Esta relación inversa resulta en una covarianza negativa entre las variables.

Impacto en el Análisis de Datos

Cuando se trabaja con datos que presentan una covarianza negativa, es crucial entender cómo esta relación afecta la interpretación de los resultados. En el ejemplo mencionado anteriormente, la presencia de una covarianza negativa entre la temperatura y la cantidad de nieve puede influir en las decisiones que se tomen basadas en estos datos. Es fundamental considerar este tipo de relaciones al realizar análisis estadísticos o proyecciones futuras.

Relación con la Correlación

Es importante mencionar que la covarianza y la correlación están estrechamente relacionadas, pero no son lo mismo. Mientras que la covarianza mide la dirección de la relación entre dos variables, la correlación indica la fuerza y dirección de la asociación entre ellas. Por lo tanto, es posible que dos variables tengan una covarianza negativa pero una correlación cercana a cero, lo que sugiere una relación débil entre las variables, a pesar de que se muevan en direcciones opuestas.

Usos en Diversos Campos

La presencia de covarianza negativa no se limita a un solo campo o disciplina. Esta relación inversa entre variables puede observarse en diversas áreas, desde la economía hasta la biología. Por ejemplo, en economía, es común encontrar una covarianza negativa entre el precio de un bien y la cantidad demandada; a medida que el precio sube, la cantidad demandada tiende a disminuir.

Importancia de la Interpretación Correcta

Para realizar análisis de datos precisos y tomar decisiones informadas, es esencial interpretar correctamente la covarianza y otros indicadores estadísticos. Una covarianza negativa no siempre implica una relación directa causal entre las variables y es fundamental considerar otros factores que puedan influir en esta asociación. La comprensión profunda de estos conceptos permite una interpretación más acertada de los datos.

Conclusión

En resumen, la covarianza puede ser negativa debido a la presencia de una relación inversa entre dos variables analizadas. Esta medida estadística ofrece información valiosa sobre cómo se comportan las variables entre sí y es fundamental para la interpretación adecuada de los datos. Al comprender la covarianza y su posible signo negativo, los analistas pueden realizar análisis más precisos y extraer conclusiones significativas de los conjuntos de datos examinados.

Preguntas Frecuentes sobre Covarianza Negativa

¿Cómo se diferencia la covarianza de la correlación?

La covarianza y la correlación son medidas estadísticas relacionadas, pero la covarianza simplemente indica la dirección de la relación entre variables, mientras que la correlación también considera la fuerza de esa relación.

¿Por qué es importante tener en cuenta la covarianza negativa en el análisis de datos?

La covarianza negativa proporciona información crucial sobre la relación entre variables, lo que puede influir en la interpretación de los resultados y en la toma de decisiones basadas en los datos analizados.